Today’s ACT question of the day involves a triangle with two equal sides. Triangles with two equal sides (and, therefore, two equal angles) are isosceles triangles. This is a key observation to make before taking on this problem.

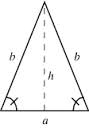
We have an isosceles triangle with only a base (length of 10). The height has been drawn in, bisecting the third angle and meeting the base at a right angle, but we don’t know its length. It would be nice if we did, right? Area of a triangle = 1/2 • base • height.

If we knew any of the angle measures, maybe we could luck out and find a 45-45-90 or 30-60-90 triangle somewhere in the diagram. We could also be sharp and recall one of our Pythagorean triplets: 3, 4, 5. Unfortunately, we don’t have any facts to support those guesses. We do have answer choices that work if you make those spurious assumptions, so be careful! Don’t make things up just to make the problem seem easier.

We could try to use trigonometry creatively to derive the hypotenuse, then work backward to find the height. Unfortunately, cos90 = 0, so that ends right there. If we knew the angle at the top of the triangle, we could use the sin of that angle • half the square of the length of one of the equal sides to find the area (works for all isosceles triangles)…but we have neither measure. What now?

I filed this problem under “esoteric” because there is a little-known way to find the area of an isosceles triangle when only the base is known.

Kidding!

There is NO way to solve this ACT problem without one of the following: the height, the side length, or one of the angles. Luckily, that’s one of our answer choices. But I’m keeping it under esoteric to remind you that it is possible to find the area of an isosceles triangle with just one side and one angle…thanks to trig. (SAT students – exhale now, there’s no trig on your test.)

Remember the area formulas, remember your types of triangles (right, special right, isosceles), remember sohcahtoa, and remember that it’s ok to choose “not enough info” if you’ve tried all the logical options and don’t have enough information to solve the problem.