Here’s today’s SAT question of the day, which is a math question about triangles and circles:
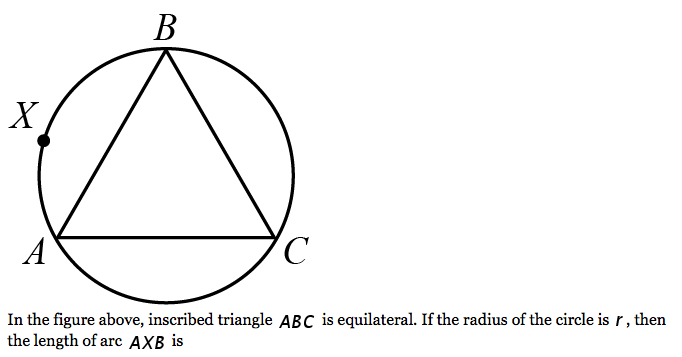
Hint: why do they tell us that ABC is equilateral? Continue reading
Category Archives: Math
SAT Question of the Day Explained – September 28, 2015 – Math, Algebra
The SAT question of the day is a math question that goes like this:
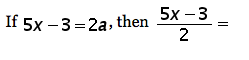
The game: substitution. Continue reading
SAT Question of the Day – September 25, 2015 – Math, Number Properties
Today’s SAT question of the day is a math question about number properties (evens and odds, in this case):
How do we make an odd into an even? Continue reading
SAT Question of the Day Explained – July 30 2015 – Math, Number Concepts, Factors, Divisibility
Today’s SAT question of the day: All numbers divisible by both 4 and 15 are also divisible by which of the following?
Divisibility…what does it mean? Just that a number can be divided evenly (no remainder) by another number. For instance, 10 is evenly divisible by 5, but not by 7. Got it?
Good. Let’s tackle today’s divisibility questions.
SAT Question of the Day Explained – January 4, 2015
Happy new year! Today’s SAT question of the day is a math question about stamps and envelopes. How many more years before no one will know what those are?? Anyhow, the question is as follows:
A machine can insert letters in envelopes at the rate of 120 per minute. Another machine can stamp the envelopes at the rate of 3 per second. How many such stamping machines are needed to keep up with 18 inserting machines of this kind?
They’ve kindly underlined the first thing that we need to look at: we have a units mismatch. One machine is in envelopes per minute, but the other is in envelopes per second. Continue reading
SAT Question of the Day Explained – December 9, 2014 – Math
Today’s SAT question of the day is a math question about some basic algebra. The answer choices are those fun roman numeral options. The question:
If 
, the value of 
can be which of the following?
. 
. 
. 
We can solve this either by doing a little algebra or by thinking it through (and testing out the answer choices). I will show you both ways. Continue reading
SAT Question of the Day Explained – December 3, 2014 – Math
Today’s SAT Question of the Day is a math question about counting. These simplistic questions often contain more than meets the eye – and this one is testing your knowledge of a simple rule of counting.
On the last day of a one-week sale, customers numbered 149 through 201 were waited on. How many customers were waited on that day?
I bet most of you just subtracted 149 from 201, bubbled in 52, and moved on. But what if I told you that isn’t the answer? Continue reading
SAT Question of the Day Explained – November 27, 2014 – Math, Algebra
Today’s SAT question of the day is an algebra question about the following quadratic equation:
Given that this equation contains the points (-2, 0) and (6, 0), we are asked to find c.
There are multiple ways of solving this, but I will show you the shortest. The first step is to think about the information we are given: why do they give us these two points?
SAT Question of the Day Explained – October 25, 2014 – Math
Today’s SAT question of the day is a fun math question that reviews some geometry basics. You’ll definitely need those basics for your test, so let’s give this one a try.
We are told that the radius of circle O is 5 and that the area of the shaded region is 20pi. X is what we are seeking.
Since the area of a circle is pi * the radius squared, we know that the whole circle’s area is 25pi. Let’s also remember that there are 360 degrees in a circle. Continue reading
SAT Question of the Day Explained – October 19, 2014 – Math, Probability
Today’s SAT question of the day is an excellent review of probability. You will probably encounter 2-3 probability questions on your SAT, so take advantage of these points if you can.
The question:
Of 5 employees, 3 are to be assigned an office and 2 are to be assigned a cubicle. If 3 of the employees are men and 2 are women, and if those assigned an office are to be chosen at random, what is the probability that the offices will be assigned to 2 of the men and 1 of the women?
Where to start? As with all probability problems, we need to find the number of total possible outcomes and the number of desired outcomes so that we can get our fraction of desired/possible.
At the beginning of our selection process, we have a total of 5 workers. Imagine that our workers are named A, B, C, D, and E. How many unique three-person combinations can we make out of A, B, C, D, and E? Let’s check:
ABC
ABD
ABE
ACD
ACE
ADE
BCD
BCE
BDE
CDE
Ten groupings it is. So, we have 10 possible outcomes. Continue reading